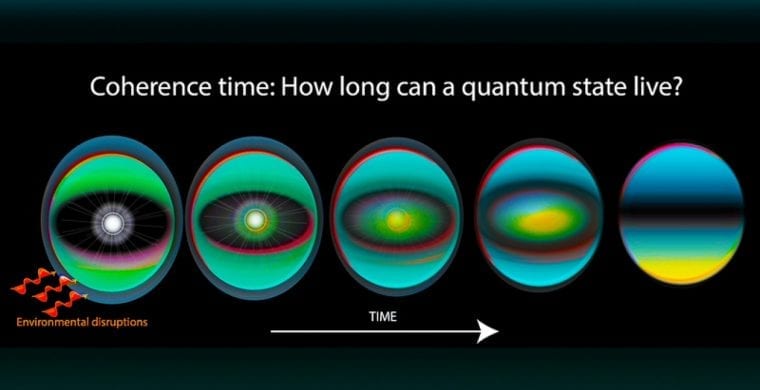
A perfect spoilsport to quantum computing is a phenomenon known as Quantum decoherence. Quantum error correction focuses on fending off decoherence and counter other errors that make quantum computing challenging.
Sources of Decoherence
For quantum computers to function, the biggest challenge is to remove or at least control quantum decoherence. But, why does it occur in the first place? The primary source is the interaction of a system with its environment; so, isolating the system from its environment is a good solution. There still exist, however, other potential sources. For example, quantum gates, lattice vibrations, and background thermonuclear spin of the physical system that is used to implement the qubits in a quantum computer.
Controlling Decoherence
Decoherence is irreversible because it is non-unitary. Avoiding it altogether is extremely difficult; therefore, tightly controlling it is the next best option. Decoherence times for candidate systems, in particular the transverse relaxation time T2 (for NMR and MRI technology, also called the dephasing time) are usually in the nanoseconds and seconds ranges at low temperature. Therefore, temperature too plays a key role—for example, as of today, some quantum computers need their qubits operating at 20 millikelvins—in managing it.
These issues are more difficult for optical approaches. This is because the timescales are of shorter magnitude, and overcoming them is a popular approach called optical pulse shaping. The ratio of operating time to decoherence time is a key measure. The goal is to make former as low as possible compared to the latter. Thus, the goal is to make the ratio minimum, thereby reducing the error rate.
Quantum error correction can be used to correct errors caused due to decoherence. However, it is possible only if the error rate is small enough. Quantum error correction, therefore, allows the total calculation time to be longer than the decoherence time. A desired error rate in each gate is 10−4 (1/10000). This translates to each gate performing its task in 10,000 times faster than the decoherence time.
Cost Considerations
A wide range of systems can meet this scalability condition. However, error correction directly translates to escalated cost due to the greatly increased number of required bits. The number required to factor integers using Shor’s algorithm is still polynomial, and between L and L2, where L is the number of bits in the number to be factored. Error correction algorithms would bump up this figure by an additional factor of L. For a 1000-bit number, this implies a need for about 104 bits without error correction. If we use error correction, the number of bits required is about 107 bits. Computation time is about L2 or about 107 steps, which at 1 MHz, which comes out to be about 10 seconds.
Countering Decoherence using Anyons
New approaches to counter the decoherence problem are always sought. One such approach is to create a topological quantum computer using anyons. Anyons are a type of quasiparticles that can occur only in two-dimensional systems. In this approach, a topological quantum computer, which is a theoretical quantum computer, uses anyons as threads and braid theory is used to form stable logic gates.
Anyons, which are a type of quasiparticles, have their world lines pass around one another to form braids in a three-dimensional space-time. The 3D space-time has one temporal and two spatial dimensions. The quantum computer is made up of various logic gates; the logic gates, in turn, are made up of these braids. A quantum computer based on quantum braids is much more stable than the one based on trapped quantum particles.
Learn more: https://amyxinternetofthings.com/